Na początek
przyjrzyjmy się z perspektywy naukowców
właśnie kwestii odbioru muzyki. Z fizycznego punktu
widzenia dźwięk jest falą rozchodzącą się w powietrzu.
Ludzkie ucho posiada zdolność określania częstotliwości
słyszanego dźwięku, co przekłada się na nasze odczucia,
kiedy słuchamy muzyki. Nazwy dźwięków: C, C♯,
D, D♯, E itd., są w istocie stałymi oznaczającymi
określone częstotliwości fal. Przykładowo dźwięk
podstawowy A1
to dźwięk o częstotliwości 440 Hz. Ten
sam dźwięk zagrany o oktawę wyżej ma częstotliwość
dwukrotnie wyższą. I tak np. dźwięk A2
(tzw. druga
harmoniczna dla tonu podstawowego A1
) to 880Hz. Co
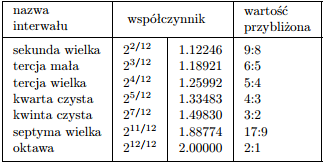
zaś z częstotliwością pozostałych dźwięków? Okazuje
się, że możemy je obliczyć wiedząc, że w stosowanej
współcześnie skali muzycznej stosunek częstotliwości
dwóch kolejnych (tj. odległych od siebie o
półton)
dźwięków jest stały. Zatem skoro podniesienie dźwięku
o jedną oktawę (12 półtonów) daje dwukrotny
wzrost
częstotliwości, to pojedynczy półton musi oznaczać
wzrost częstotliwości o czynnik 12√
2. Stąd możemy już
łatwo wyliczyć częstotliwości wszystkich dźwięków.
Jak jednak przekłada się to na przyjemność płynącą
z odbioru muzyki będącej kombinacją dźwięków?
Otóż okazuje się, o czym wiedzieli już Pitagorejczycy,
że człowiek odbiera jako harmonijne zestawienie
takich dźwięków, których częstotliwości pozostają
ze sobą w stosunku będącym ilorazem niewielkich
liczb naturalnych. [Pitagorejczycy zauważyli, że jeżeli
długości dwóch napiętych jednakową siłą strun mają się
jak 1:2, to struny te dają przyjemne współbrzmienie.
Podobnie 2:3, 3:4 – te zależności są liczbowym opisem
konkretnych interwałów muzycznych: oktawy (1:2),
kwinty czystej i kwarty czystej. Ich obserwacje można
streścić w stwierdzeniu, że „harmonia wyraża się
przez stosunek dwóch liczb naturalnych i tym jest
pełniejsza, im liczby te są mniejsze”.